cs231n作业2笔记

简介

Assignment1中我们分别采用 kNN、线性分类器、SVM、Softmax分类以及简单两层神经网络对CIFAR-10数据集进行了分类。

来到Assignment2中，需要自己搭建卷积神经网络（CNN）来进行图像分类。

Assignment2主要分为5个部分：

• Fully-connected Nerual Network

这部分为作业1中两层神经网络的延续，需要将各个隐藏层的forward以及backward过程模块化，以便搭建任意层数的神经网络。

• Batch Normalization

为了使深度神经网络的训练更快，一种策略是寻找更好的优化方法；另一种思路便是改变网络的架构使其训练更快。我们知道，机器学习方法对于白化（特征之间无相关性，零均值，单位方差）的输入数据有着更好的效果。

对数据的预处理（去均值、归一化、PCA以及白化）只能保证第一层的输入满足条件，但随着网络的逐步深入，深层网络的激活输入就不再满足条件了。更糟的是，随着训练加深，每层的特征分布还会随着权重的更新而偏移。

loffe 2015提出的Batch Normalization便是为了解决这个问题的。具体可以参考论文。

• Dropout

Dropout 是缓解过拟合的一种方法。会按比例随机的丢掉一部分激活值，达到缓解过拟合的目的。

• Convolutional Networks

这部分需要完成CNN的各个组件，然后组合在一起，搭建一个完整的CNN网络。

• PyTorch/TensofFlow on CIFAR-10

主要是这两个框架的练习。

我的代码实现whu-pzhang/cs231n.

Fully-connected Nerual Network

这部分需要对每层实现一个 forward 和 backward 函数：forward 函数接收为输入、权重和其他参数，返回输出以及一个 cache 对象，包含反向传播计算梯度时用到的数据。

def layer_forward(x, w):
  """ Receive inputs x and weights w """
  # Do some computations ...
  z = # ... some intermediate value
  # Do some more computations ...
  out = # the output

  cache = (x, w, z, out) # Values we need to compute gradients

  return out, cache

backward 函数则接收upstream传过来的梯度和 forward 返回的 cache 对象， 计算返回该层相对于输入和权重的梯度值。

def layer_backward(dout, cache):
  """
  Receive dout (derivative of loss with respect to outputs) and cache,
  and compute derivative with respect to inputs.
  """
  # Unpack cache values
  x, w, z, out = cache

  # Use values in cache to compute derivatives
  dx = # Derivative of loss with respect to x
  dw = # Derivative of loss with respect to w

  return dx, dw

affine layer

全连接层的forward就是简单的矩阵乘法。需要先将每个实例展平为向量，然后和权重做矩阵乘法即可，最后别忘了偏置项。

x_reshaped = x.reshape(x.shape[0], -1)
out = x_reshaped.dot(w) + b

backward时，根据链式法计算即可，注意各个量的shape即可。

dx = dout.dot(w.T).reshape(*x.shape)
dw = x.reshape(x.shape[0], -1).T.dot(dout)
db = np.sum(dout, axis=0)

ReLU activation

ReLU 激活只是应用一个mask，计算相当简单，直接用 np.maximum() 函数即可。

backward时，注意只有大于零的项有梯度值。

组合层

将affine层和ReLU组合起来即可

loss layers

在作业1中实现的Softmax和SVM损失函数可以直接拿过来用，不再赘述。

搭建多层神经网络

现在直接将前面实现的层组合起来便可以实现全连接层神经网络。 搭建完成后，利用提供的Solver类，便可以实现神经网络的训练和验证。

优化方法

根据讲义里的各种优化方法，直接实现即可，没啥难度。主要是理解每个优化方法的思想。 依次是 SGD+Momentum，RMSProp 和 Adam。

Batch Normalization

Batch Normalization是为了克服层数较多的神经网络在训练时的 internal covariate shift 现象，减弱梯度饱和。此外，还可以加快训练速度，学习率也可以设置的较大。

forward

设BN层的小批量输入为 $\boldsymbol{X} \in \mathbb{R}^{ N \times D}$。 在forward过程中，首先计算每个特征的均值和方差：

\[ \begin{align} \boldsymbol{\mu} &= \frac{1}{N} \sum_{k=1}^N \boldsymbol{x}_k \\ \boldsymbol{\sigma}^2 & = \frac{1}{N} \sum_{k=1}^N { (\boldsymbol{x}_k - \boldsymbol{\mu})^2 } \end{align} \]

接着就可以对输入进行归一化：

\[ \boldsymbol{\hat{x}}_i = \frac{ \boldsymbol{x}_i - \boldsymbol{\mu}} { \sqrt{\boldsymbol{\sigma}^2 + \epsilon} } \]

再进行平移和缩放：

\[ \boldsymbol{y}_i = \gamma \, \boldsymbol{\hat x}_i + \beta \]

其中，$\gamma, \beta \in \mathbb{R}^{1 \times D}$。整个forward过程可记为：

\[ \boldsymbol{\hat{X}} = \frac{\boldsymbol{X} - \boldsymbol{\mu}} {\sqrt{ \boldsymbol{\sigma}^2 + \epsilon}} \\ \boldsymbol{Y} = \gamma \odot \boldsymbol{\hat{X}} + \beta \]

至此，正向传播就完成了。

为了方便计算梯度的反向传播，根据计算图可将forward过程分解为如下9步：

mu = 1.0 / N * np.sum(x, axis=0, keepdims=True)               # (1)
xsubmu = x - mu                                               # (2)
xsubmusqr = xsubmu**2                                         # (3)
var = 1.0 / N * np.sum(xsubmusqr, axis=0, keepdims=True)      # (4)
sqrtvar = np.sqrt(var + eps)                                  # (5)
invsqrtvar = 1.0 / sqrtvar                                    # (6)
x_norm = xsubmu * invsqrtvar                                  # (7)
gammax = gamma * x_norm                                       # (8)
out = gammax + beta                                           # (9)

backward

backward 过程按照上面9步倒序进行即可：

dgammax = dout                                                # (9)
dbeta = np.sum(dout, axis=0, keepdims=True)                   # (9)
dgamma = np.sum(dgammax * x_norm, axis=0, keepdims=True)      # (8)
dx_norm = dgammax * gamma                                     # (8)
dxsubmu = dx_norm * invsqrtvar                                # (7)
dinvsqrtvar = np.sum(dx_norm * xsubmu, axis=0, keepdims=True) # (7)
dsqrtvar = dinvsqrtvar * (-1.0) * (sqrtvar)**(-2)             # (6)
dvar = dsqrtvar * (0.5 * (var + eps)**(-0.5))                 # (5)
dxsubmusqr = dvar * (1.0 / N * np.ones((N, D)))               # (4)
dxsubmu += dxsubmusqr * (2 * xsubmu)                          # (3)
dx = dxsubmu                                                  # (2)
dmu = -1.0 * np.sum(dxsubmu, axis=0, keepdims=True)           # (2)
dx += dmu * (1.0 / N * np.ones((N, D)))                       # (1)

Alternative backward implement

BatchNorm backward前面的实现是按照计算图一步步来的，实际上可以直接推导出BatchNorm的梯度计算公式，这样能够简化计算。

设 $L$ 为训练损失，我们已知从upstream传来的 $\frac{\partial L}{\partial \boldsymbol{Y}} \in \mathbb{R}^{N \times D}$， 反向传播时，我们需要计算：

1. $\frac{\partial L}{\partial \beta} \in \mathbb{R}^{1 \times D}$
2. $\frac{\partial L}{\partial \gamma} \in \mathbb{R}^{1 \times D}$
3. $\frac{\partial L}{\partial \boldsymbol{X}} \in \mathbb{R}^{N \times D}$。

$\frac{\partial L}{\partial \beta}$ 和 $\frac{\partial L}{\partial \gamma}$ 的计算很直观：

\[ \begin{align} \frac{\partial L}{\partial \gamma} & = \sum_{i}^N { \frac{\partial L} {\partial \boldsymbol{y}_i} \odot \boldsymbol{\hat{x}_i}} \\ \frac{\partial L}{\partial \beta} & = \sum_i^N {\frac{\partial L} {\partial \boldsymbol{y}_i}} \end{align} \]

而 $\frac{\partial L}{\partial \boldsymbol{x}_i}$ 的计算则比较复杂。 由于 $\boldsymbol{\mu}, \boldsymbol{\sigma}$ 都是 $\boldsymbol{x}_i$ 的函数，根据链式法则：

\[ \frac{\partial L}{\partial \boldsymbol{x}_i} = \frac{\partial L}{\partial \boldsymbol{\hat{x}}_i} \frac{\partial \boldsymbol{\hat{x}}_i}{\partial \boldsymbol{x}_i} + \frac{\partial L}{\partial \boldsymbol{\sigma}^2} \frac{\partial \boldsymbol{\sigma}^2}{\partial \boldsymbol{x}_i} + \frac{\partial L}{\partial \boldsymbol{\mu}} \frac{\partial \boldsymbol{\mu}}{\partial \boldsymbol{x}_i} \]

我们可以依次计算这三项。第一项比较简单：

\[ \begin{align} \frac{\partial L}{\partial \boldsymbol{\hat{x}}_i} & = \gamma \odot \frac{\partial L}{\partial \boldsymbol{y}_i} \\ \frac{\partial \boldsymbol{\hat{x}}_i}{\partial \boldsymbol{x}_i} & = (\boldsymbol{\sigma}^2 + \epsilon) ^ {-1/2} \\ & \Downarrow \\ \frac{\partial L}{\partial \boldsymbol{\hat{x}}_i} \frac{\partial \boldsymbol{\hat{x}}_i}{\partial \boldsymbol{x}_i} & = \gamma \odot \frac{\partial L}{\partial \boldsymbol{y}_i} \, (\boldsymbol{\sigma}^2 + \epsilon) ^ {-1/2} \end{align} \]

接下来计算第二项：

\[ \frac{\partial L}{\partial \boldsymbol{\sigma}^2} = \sum_i^N { \frac{\partial L}{\partial \boldsymbol{\hat{x}}_i} \, \frac{\partial \boldsymbol{\hat{x}}_i}{\partial \boldsymbol{\sigma}^2} } = -\frac{\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-3/2}}{2} \, \sum_{i}^{N} {\frac{\partial L}{\partial \boldsymbol{y}_i} \odot (\boldsymbol{x}_i - \boldsymbol{\mu}) } \]

计算相对于 $\boldsymbol{\sigma}$ 的梯度时，需要沿着批量中所有的实例求和，对 $\boldsymbol{\mu}$ 求导（第三项）时也是一样：

\[ \begin{align} \frac{\partial L}{\partial \boldsymbol{\mu}} & = \sum_i^N { \frac{\partial L}{\partial \boldsymbol{\hat{x}}_i} \frac{\partial \boldsymbol{\hat{x}}_i}{\partial \boldsymbol{\mu}} } + \frac{\partial L}{\partial \boldsymbol{\sigma}^2} \frac{\partial \boldsymbol{\sigma}^2}{\partial \boldsymbol{\mu}} \\ & = -\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-1/2} \, \sum_{i}^{N} {\frac{\partial L}{\partial \boldsymbol{y}_i}} + \frac{\partial L}{\partial \boldsymbol{\sigma}^2} \cdot (-\frac{2}{N}) \cdot \sum_i^N (\boldsymbol{x}_i - \boldsymbol{\mu}) \\ & = -\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-1/2} \, \sum_{i}^{N} {\frac{\partial L}{\partial \boldsymbol{y}_i}} \end{align} \]

接下来分别求得 $\frac{\partial \boldsymbol{\sigma}^2}{\partial \boldsymbol{x}_i}$ 和 $\frac{\partial \boldsymbol{\mu}}{\partial \boldsymbol{x}_i}$:

\[ \frac{\partial \boldsymbol{\mu}} {\partial \boldsymbol{x}_i} = \frac{1}{N} \\ \frac{\partial \boldsymbol{\sigma}^2} {\partial \boldsymbol{x}_i} = \frac{2}{N} \sum_i^N (\boldsymbol{x}_i - \boldsymbol{\mu}) \]

现在可得第二项为：

\[ \begin{align} \frac{\partial L}{\partial \boldsymbol{\sigma}^2} \frac{\partial \boldsymbol{\sigma}^2}{\partial \boldsymbol{x}_i} & = -\frac{\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-3/2}}{2} \, \sum_{i}^{N} {\frac{\partial L}{\partial \boldsymbol{y}_i} \odot (\boldsymbol{x}_i - \boldsymbol{\mu}) } \cdot \frac{2}{N} (\boldsymbol{x}_j - \boldsymbol{\mu}) \\ & = -\frac{\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-1/2}} {N} \left( \sum_i^N {\frac{\partial L}{\partial \boldsymbol{y}_i} \odot (\boldsymbol{x}_i - \boldsymbol{\mu}) } \right) \frac{ \boldsymbol{x}_j - \boldsymbol{\mu}} {\boldsymbol{\sigma}^2 + \epsilon} \\ & = -\frac{\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-1/2}} {N} \left( \sum_i^N {\frac{\partial L}{\partial \boldsymbol{y}_i} \odot \boldsymbol{\hat{x}_i}\sqrt{\boldsymbol{\sigma}^2 + \epsilon} } \right) \frac{ \boldsymbol{x}_j - \boldsymbol{\mu}} {\boldsymbol{\sigma}^2 + \epsilon} \\ & = -\frac{\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-1/2}} {N} \left( \sum_i^N {\frac{\partial L}{\partial \boldsymbol{y}_i} \odot \boldsymbol{\hat{x}_i} } \right) \frac{ \boldsymbol{x}_j - \boldsymbol{\mu}} { \sqrt{\boldsymbol{\sigma}^2 + \epsilon} } \\ & = -\frac{\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-1/2}} {N} \cdot \frac{\partial L} {\partial \gamma} \cdot \boldsymbol{\hat{x}_j} \end{align} \]

第三项为：

\[ \begin{align} \frac{\partial L}{\partial \boldsymbol{\mu}} \frac{\partial \boldsymbol{\mu}}{\partial \boldsymbol{x}_i} & = -\frac{\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-1/2}} {N} \cdot \sum_i^N { \frac{\partial L} {\partial \boldsymbol{y}_i}} \\ & = -\frac{\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-1/2}} {N} \cdot \frac{\partial L} {\partial \beta} \end{align} \]

现在将这三项加在一块即可得：

\[ \frac{\partial L}{\partial \boldsymbol{x}_i} = \frac{\gamma (\boldsymbol{\sigma}^2 + \epsilon)^{-1/2}} {N} \left( N \frac{\partial L} {\partial \boldsymbol{y}_i} - \frac{\partial L} {\partial \gamma} \cdot \boldsymbol{\hat{x}_j} - \frac{\partial L} {\partial \beta} \right) \]

最终我们得到了$\frac{\partial L}{\partial \boldsymbol{x}_i}$的数学表达式，相比前面基于计算图的实现更为简便。实现代码如下：

xsubmu, var, sqrtvar, invsqrtvar, x_norm, gamma, eps = cache
N, D = xsubmu.shape
dbeta = np.sum(dout, axis=0, keepdims=True)
dgamma = np.sum(x_norm * dout, axis=0, keepdims=True)
dx = (1. / N) * gamma * invsqrtvar * (N * dout - dgamma * x_norm - dbeta)

这个实现相比基于计算图的实现，会快上2~4倍。

Layer Normalization

BatchNorm对batch size的依赖使其在复杂网络的训练中受限。因此发展出了多种batchnorm的变种。 Layer Normalization 是沿着特征轴进行的 Batch Normalization。其实现只需要对batchnorm进行些许的改动即可。

Dropout

Dropout是在forward过程中通过随机将一部分特征设为零来实现的一种正则化方法。实现起来也很简单，不过为了使测试时的代码不发生改变，通常使用的是 Inverted dropout，在训练时进行放大。

mask = (np.random.rand(*x.shape) < p) / p
out = x * mask

Convolutional Networks

卷积神经网络（CNN）其实和常规的神经网络很像，由包含可学习的权重和偏置的神经元组成。 每个神经元参数与输入做点积得到新的输出。CNN中通常包括卷积层（Convolutional layer）、池化层（Pooling layer）和全联接层（Fully-connected layer）。

卷积层是CNN的核心。在处理图像这类高维的输入时，不可能将当前神经元与输入的全部神经元连接起来。在卷积层中，只将当前神经元与输入数据的局部区域进行连接。即神经元的局部感受野（Local receptive field），也即是卷积核的大小，这是一个Hyperparameter。此外，主要注意的是，这种空间局部连接在深度轴方向总是与输入的深度相等的。

卷积层的输出大小由三个Hyperparameter控制：

1. 输出深度（depth）：对应着卷积层中卷积核的个数。每个卷积核在训练过程中会从输入中提取出不同的特征。

2. 滑动步幅（stride）：控制着卷积核每次移动的像素数。当stride为2时，卷积核每次移动两个像素。

3. zero-padding：输入数据边缘需要填充的大小。可以控制输出的空间大小。

输出的空间大小是着三个参数的函数。设输入数据大小为 $W$，卷积层神经元感受野大小为$F$，卷积核移动步幅为$S$，zero-padding大小为$P$，那么该卷积层输出的大小为

\[ (W - F + 2P) / S + 1 \]

卷积层的另外一个重要特点是权值共享（weight sharing），也就是说对同一层的每个神经元的权重都是同一个，这样可使网络的参数大大减少。

作业2中的卷积采用的是原始实现，通过两层循环即可，这里不多讲，直接贴我的代码实现：

forward：

stride = conv_param['stride']
pad = conv_param['pad']
N, C, H, W = x.shape
F, C, HH, WW = w.shape
Hout = (H + 2 * pad - HH) // stride + 1
Wout = (W + 2 * pad - WW) // stride + 1
out = np.zeros((N, F, Hout, Wout), dtype=x.dtype)

padx = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant')
for i in range(Hout):
    for j in range(Wout):
        xblock = padx[:, :, i * stride:i *
                      stride + HH, j * stride:j * stride + WW]
        for k in range(F):
            out[:, k, i, j] = np.sum(xblock * w[k], axis=(1, 2, 3))

out += b[np.newaxis, :, np.newaxis, np.newaxis]

backward:

dw = np.zeros_like(w)
dpadx = np.zeros_like(padx)
db = np.sum(dout, axis=(0, 2, 3))
for i in range(Hout):
    for j in range(Wout):
        xblock = padx[:, :, i * stride:i *
                      stride + HH, j * stride:j * stride + WW]
        for k in range(F):
            dw[k, :, :, :] += np.sum(xblock * dout[:, k, i, j]
                                     [:, None, None, None], axis=0)
        for n in range(N):
            dpadx[n, :, i * stride:i * stride + HH, j * stride:j * stride +
                  WW] += np.sum(dout[n, :, i, j][:, None, None, None] * w, axis=0)

im2col

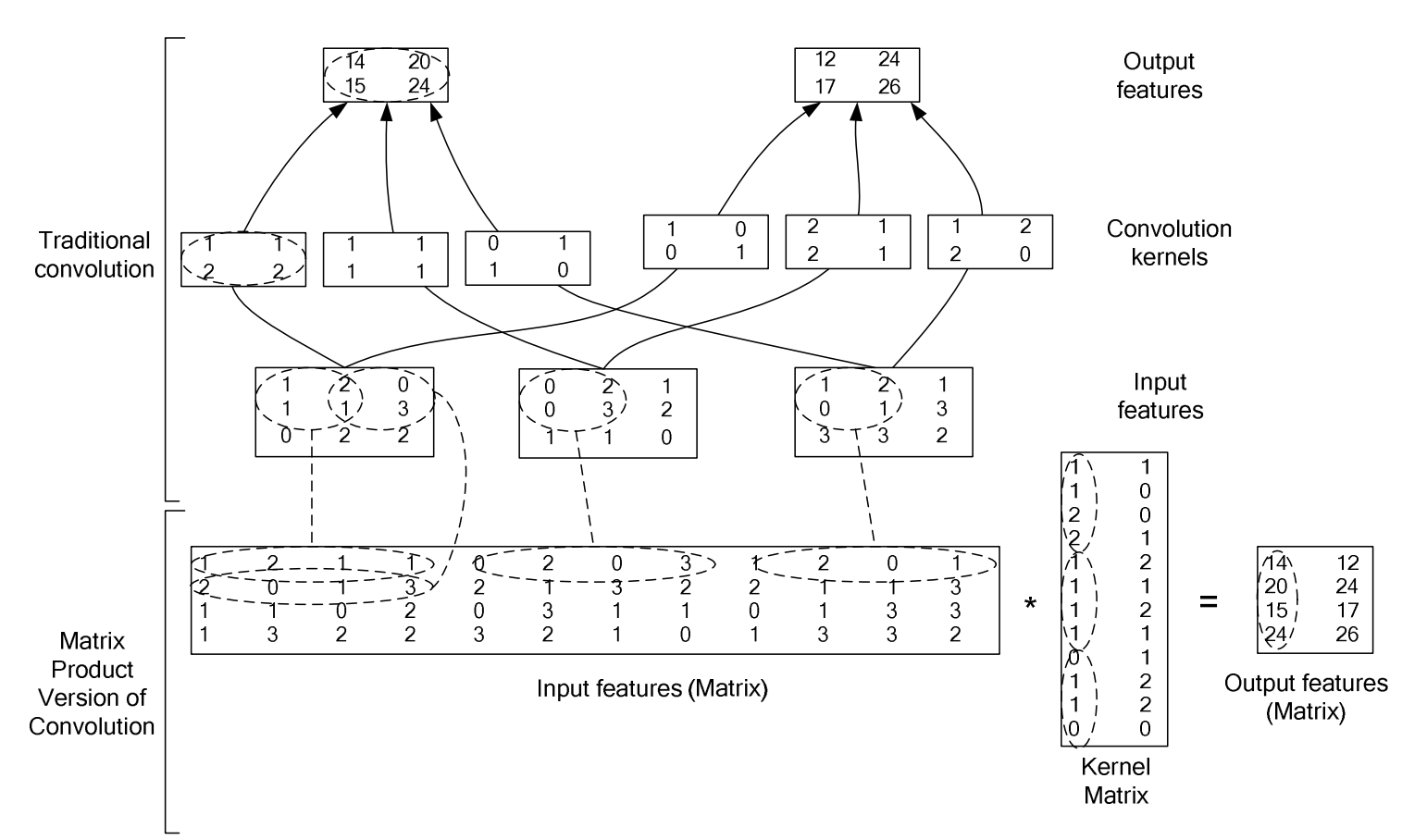
这里来推导CNN基于矩阵乘法的高效实现。 先来看单通道的情况。为了简单起见， 设输入$X$ 为 $3 \times 3$，卷积核$W$为 $2 \times 2$，步幅为1，没有pading，那么输出$Y$的大小为 $(3 - 2)/1 + 1 = 2$。在实际计算中，为了提高效率，通常会把二维卷积转为矩阵乘法，这样就避免了循环。具体就是先将输入中卷积核对应的每个局部感受野展平为向量，然后叠成一个大的矩阵，矩阵的大小计算根据输出大小和卷积核大小确定：本例中，输出为 $2 \times 2$，展平即为 $4 \times 1$，卷积核大小为 $2 \times 2$，展平为 $4 \times 1$，因此输入 $X$ 会变成 $4 \times 4$ 的矩阵，记为 $X_{col}$，这个操作称为 im2col: \( \begin{pmatrix} x_{11} & x_{12} & x_{13} \\ x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} & x_{33} \end{pmatrix} \xrightarrow{\mathrm{im2col}} \begin{pmatrix} x_{11} & x_{12} & x_{21} & x_{22} \\ x_{12} & x_{13} & x_{22} & x_{23} \\ x_{21} & x_{22} & x_{31} & x_{32} \\ x_{22} & x_{23} & x_{32} & x_{33} \end{pmatrix} \)

如此一来，卷积就变为了矩阵乘：

\[ \begin{align} X \otimes W = X_{col} \, W_{col} & = \begin{pmatrix} x_{11} & x_{12} & x_{21} & x_{22} \\ x_{12} & x_{13} & x_{22} & x_{23} \\ x_{21} & x_{22} & x_{31} & x_{32} \\ x_{22} & x_{23} & x_{32} & x_{33} \end{pmatrix} \begin{pmatrix} w_{11} \\ w_{12} \\ w_{21} \\ w_{22} \end{pmatrix} \\ & = \begin{pmatrix} x_{11} w_{11} + x_{12} w_{12} + x_{21} w_{21} + x_{22} w_{22} \\ x_{12} w_{11} + x_{13} w_{12} + x_{22} w_{21} + x_{23} w_{22} \\ x_{21} w_{11} + x_{22} w_{12} + x_{31} w_{21} + x_{32} w_{22} \\ x_{22} w_{11} + x_{23} w_{12} + x_{32} w_{21} + x_{33} w_{22} \\ \end{pmatrix} = \boldsymbol{Y}_{col} \end{align} \]

这样卷积层的计算就和常规的线性回归一样了，易知：

\[ \mathrm{d} {X_{col}} = \delta \ W_{col}^T \\ \mathrm{d} {W_{col}} = X_{col} \ \delta \]

其中，$\delta$ 为上游传过来的梯度。在backward过程中，求 $\mathrm{d} W$ 只需要将 $\mathrm{d} {W_{col}}$ reshape一下即可。但是求 $\mathrm{d} X$ 就不能简单的通过reshape来进行。 我们还需要将 $\mathrm{d} {X_{col}}$ 再转回二维矩阵的形式，也就是 col2im：

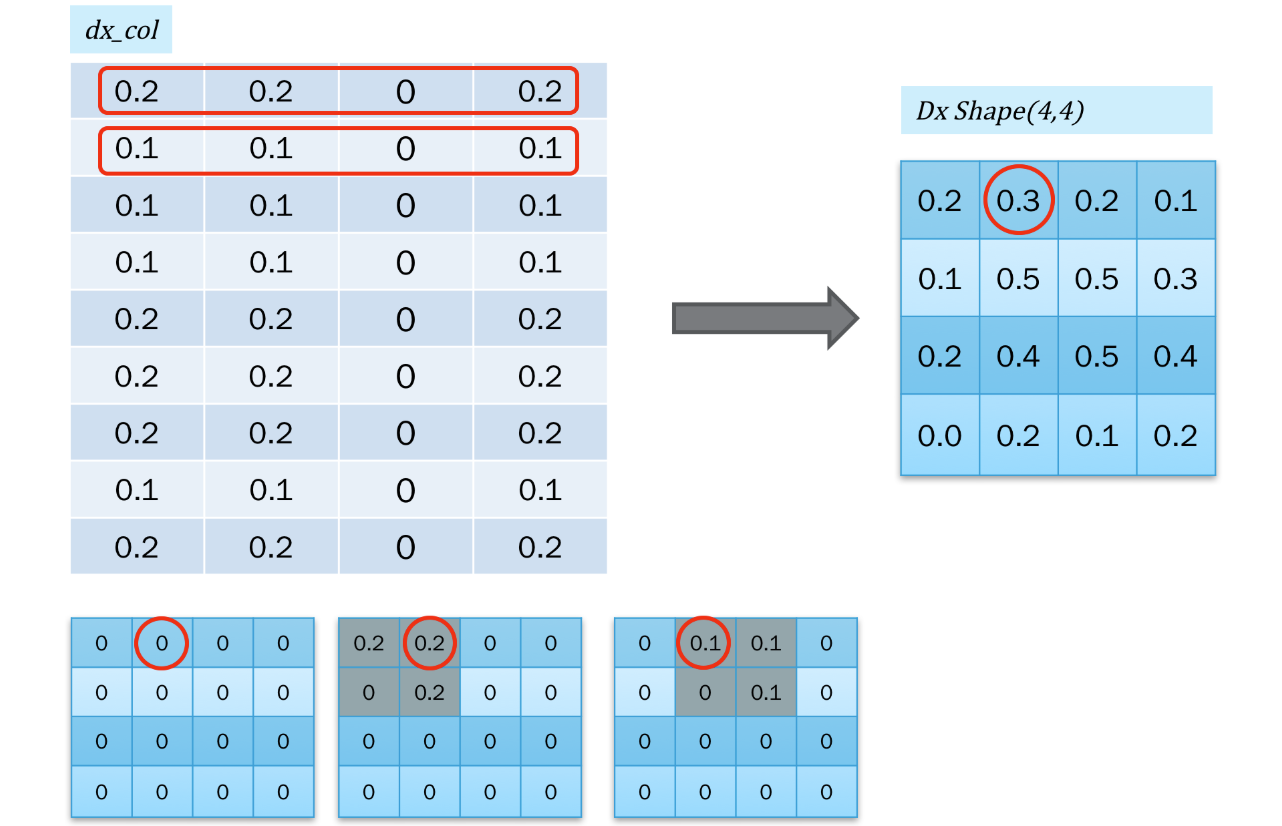
转换时，同一位置的值是不断累加的。

对于多通道输入，也是一样的原理：先将每个卷积核对应的局部感受野展平为一个列向量， 然后将卷积核展平为行向量。以AlexNet为例，输入图像形状为 $227 \times 227 \times 3$， 卷积核形状为 $11 \times 11 \times 3$，步幅为4。那么就将卷积核的每个感受野展平为 $11 \times 11 \times 3=363$ 大小的列向量。以步幅4遍历整个图像后，卷积核的输出宽和高均为 $(227-11)/4+1=55$， 展平的话就是大小$55 \times 55=3025$的行向量。那么一幅图像经 im2col 后就变换成了大小 $363 \times 3025$ 的矩阵。

卷积层的权重参数也是类似的展平为列向量，AlexNet中第一个卷积层深度为96，那么经展平后，权重就变为了 $96 \times 363$ 大小的矩阵。接下来直接进行矩阵乘法就完成了forward过程，得到的输出大小为 $96 \times 3025$，对其reshape一下就得到了输出大小 $96 \times 55 \times 55$。

新的计算公式

col2im 计算复杂度很高，计算 $\nabla X$ 通常还有其他的方法。

根据forward计算得到的结果 $Y_{col}$ 可以依次写出每个 $x_{ij}$ 的导数如下：

\[ \begin{split} \frac{\partial L} {\partial x_{11}} & = \boldsymbol{\delta} \cdot \begin{pmatrix} w_{11} & 0 \\ 0 & 0 \end{pmatrix} & = \delta_{11} w_{11} \\ \frac{\partial L} {\partial x_{12}} & = \boldsymbol{\delta} \cdot \begin{pmatrix} w_{12} & w_{11} \\ 0 & 0 \end{pmatrix} & = \delta_{11} w_{12} + \delta_{12} w_{11} \\ \frac{\partial L} {\partial x_{13}} & = \boldsymbol{\delta} \cdot \begin{pmatrix} 0 & w_{12} \\ 0 & 0 \end{pmatrix} & = \delta_{12} w_{12} \\ & & \vdots \\ \frac{\partial L} {\partial x_{22}} & = \boldsymbol{\delta} \cdot \begin{pmatrix} w_{22} & w_{21} \\ w_{12} & w_{11} \end{pmatrix} & = \delta_{11} w_{22} + \delta_{12} w_{21} + \delta_{21} w_{12} + \delta_{22} w_{11} \\ & & \vdots \\ \frac{\partial L} {\partial x_{33}} & = \boldsymbol{\delta} \cdot \begin{pmatrix} 0 & 0 \\ 0 & w_{22} \end{pmatrix} & = \delta_{22} w_{22} \end{split} \]

观察发现，可以用一个卷积来计算：

\[ \begin{pmatrix} 0 & 0 & 0 & 0 \\ 0 & \delta_{11} & \delta_{12} & 0 \\ 0 & \delta_{21} & \delta_{22} & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} * \begin{pmatrix} w_{22} & w_{21} \\ w_{12} & w_{11} \end{pmatrix} = \begin{pmatrix} \nabla x_{11} & \nabla x_{12} & \nabla x_{13} \\ \nabla x_{21} & \nabla x_{22} & \nabla x_{23} \\ \nabla x_{31} & \nabla x_{32} & \nabla x_{33} \end{pmatrix} \]

该卷积核为forward中卷积核翻转之后得到，这是对 $\delta$ 做卷积，称之为逆向卷积（有的地方称为去卷积(deconvolution)，但用在这里并不合适，deconvolution在信号和图像处理中有明确的定义，与这里的操作不同。）：

\[ \frac{\partial L} {\partial \boldsymbol{X}} = \boldsymbol{\delta} \otimes flipped(\boldsymbol{W}) \]

具体计算过程中，先对 $\delta$ 做zero-padding，然后就和forward过程一样了，通过im2col映射为 $\delta_{col}$，接着就是矩阵乘。最后将得到的 $\nabla X_{col}$ reshape 一下得到原始大小即可。

同理，$\boldsymbol{W}$ 的梯度也可以用同样的原理来计算。

Max pooling

pooling层起到下采样的作用，可以大幅度的减少网络的参数，使训练变得容易。最常用的即是max pooling。pooling层参数和卷积层相同，根据pooling的大小以及padding等参数来确定其输出的 大小，计算公式和卷积层相同。

forward时，依次处理每个pooling区域内的值，以max pooling为例，只保留pooling区域内的最大值作为输出值。若输入为 $4 \times 4$，pooling的核大小为2，stride=1，没有padding时，输出大小为 $2 \times 2$:

\[ \begin{bmatrix} 5 & 3 & 1 & 2\\ 1 & 2 & 3 & 2\\ 4 & 2 & 2 & 5\\ 3 & 6 & 1 & 1 \end{bmatrix} \Rightarrow \begin{bmatrix} 5 & 3 \\ 6 & 5 \end{bmatrix} \]

backward时，先将梯度矩阵还原为pooling前的大小，接着将梯度直接传给前一层取最大值位置处的，其他位置梯度为零，保证梯度总大小不变：

\[ \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0.8 & 0\\ 0 & 0 & 0 & 0.6\\ 0 & 0.4 & 0 & 0 \end{bmatrix} \Leftarrow \begin{bmatrix} 1 & 0.8 \\ 0.4 & 0.6 \end{bmatrix} \]

若是Average pooling层，backward时，则是将梯度平均分配到原来的位置上去：

\[ \begin{bmatrix} 0.25 & 0.25 & 0.2 & 0.2\\ 0.25 & 0.25 & 0.2 & 0.2\\ 0.1 & 0.1 & 0.15 & 0.15\\ 0.1 & 0.1 & 0.15 & 0.15 \end{bmatrix} \Leftarrow \begin{bmatrix} 1 & 0.8 \\ 0.4 & 0.6 \end{bmatrix} \]

原始实现代码如下：

forward：

for i in range(Hout):
    for j in range(Wout):
        xblock = x[:, :, i * stride:i * stride +
                    HH, j * stride:j * stride + WW]
        out[:, :, i, j] = np.max(xblock, axis=(2, 3))

Backward:

for i in range(Hout):
    for j in range(Wout):
        xblock = x[:, :, i * stride:i * stride +
                     HH, j * stride:j * stride + WW]
        max_values = np.max(xblock, axis=(2, 3), keepdims=True)
        mask = (xblock == max_values)
        dx[:, :, i * stride:i * stride +
           HH, j * stride:j * stride + WW] += dout[:, :, i, j][:, :, None, None] * mask

Spatial batch normalization

BatchNorm 不仅可以加快全连接深度神经网络的训练过程，而且对CNN也有效，只不过需要略微的调整，调整后称为 Spatial batch normalization.

BatchNorm 是沿着小批量维做归一化，输入为 $\mathbb{R}^{N \times D}$，则沿着 $N$ 方向做归一化。但是在CNN中，BatchNorm的输入大小为 $\mathbb{R}^{N \times C \times H \times W}$，$N$ 为小批量实例数目，$H \times W$ 为特征图大小。

Spatial batch normalization对每个通道 $C$ 计算均值和方差，然后对数据进行归一化。 因此，将batchnorm程序稍作修改即可：

Forward:

N, C, H, W = x.shape
x_reshaped = np.transpose(x, axes=[0, 2, 3, 1]).reshape(-1, C)
out, cache = batchnorm_forward(x_reshaped, gamma, beta, bn_param)
out = np.transpose(out.reshape((N, H, W, C)), axes=[0, 3, 1, 2])

backward:

N, C, H, W = dout.shape
dout_reshaped = np.transpose(dout, axes=[0, 2, 3, 1]).reshape(-1, C)
dx, dgamma, dbeta = batchnorm_backward(dout_reshaped, cache)
dx = np.transpose(dx.reshape((N, H, W, C)), axes=[0, 3, 1, 2])

Group normalization

LayerNorm是BatchNorm的一种缓解batchsize依赖的选择，但研究人员发现，在CNN中，LayerNorm表现不如BatchNorm。因此又提出了一种新的归一化方法： Group normalization，为LayerNorm和BatchNorm的折衷。

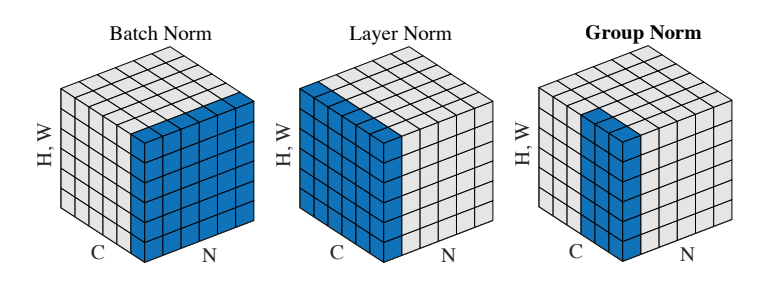
相比如LayerNorm和BatchNorm，GroupNorm多了一个控制Group的参数 G。

forward：

group_size = C // G
x_reshaped = np.transpose(x, axes=[0, 2, 3, 1]).reshape(-1, C)
gamma_reshaped = np.transpose(gamma, axes=[0, 2, 3, 1]).reshape(C,)
beta_reshaped = np.transpose(beta, axes=[0, 2, 3, 1]).reshape(C,)
for i in range(G):
    index = np.arange(i * group_size, (i + 1) * group_size)
    group_x = x_reshaped[:, index]
    group_gamma = gamma_reshaped[index]
    group_beta = beta_reshaped[index]
    group_out, group_cache = layernorm_forward(
        group_x, group_gamma, group_beta, gn_param)

    out[:, index, :, :] = np.transpose(
        group_out.reshape(N, H, W, group_size), axes=[0, 3, 1, 2])
    cache.append(group_cache)

backward:

N, C, H, W = dout.shape
dx = np.zeros_like(dout)
dgamma = np.zeros((1, C, 1, 1), dtype=dout.dtype)
dbeta = np.zeros((1, C, 1, 1), dtype=dout.dtype)
G = len(cache)
group_size = C // G
dout_reshaped = np.transpose(dout, axes=[0, 2, 3, 1]).reshape(-1, C)
for i in range(G):
    index = np.arange(i * group_size, (i + 1) * group_size)
    group_dout = dout_reshaped[:, index]
    group_cache = cache[i]
    group_dx, group_dgamma, group_dbeta = layernorm_backward(
        group_dout, group_cache)
    dx[:, index, :, :] = np.transpose(
        group_dx.reshape(N, H, W, group_size), axes=[0, 3, 1, 2])
    dgamma[:, index, :, :] = group_dgamma[:, :, None, None]
    dbeta[:, index, :, :] = group_dbeta[:, :, None, None]

总结

作业2的核心在于实现一个可用的CNN网络，重点是卷积层原理和实现以及BatchNorm层的原理和实现，作业中的卷积层采用的是原始的循环方法，是较为低效的实现，实际中一般采用 im2col 来实现，可以充分利用计算机的并行优势。而BatchNorm则是优化训练效果和速度的黑魔法，后面的LayerNorm以及GroupNorm均为其变种。